Standard O-Plan Demonstrations
Introduction
This document describes a set of demonstration applications which
can be used as an introduction to the O-Plan system. They range
in complexity from simple block stacking problems to such things
as space station construction, satellite control, and island evacuations.
The demonstrations show many aspects of planning problems, from
simple action expansions to complex, goal-directed reasoning.
For each demonstration there are a number of hypertext links that,
when selected, run O-Plan on a machine in Edinburgh using the
World-Wide Web's
Common Gateway Interface. This results in a document
that describes a plan for whatever problem ("task") the link you
selected represents.
Instead of saying "applications", we'll often talk of domains.
Informally, a domain is just a planning application area such as
house-building or block-stacking. However, we'll also use "domain"
in a narrower, technical sense to refer to a set of definitions
prepared for O-Plan. Such domains are also called "domain descriptions",
or "domain definitions" and are written in the Task Formalism (TF)
language. More than one set of definitions can be written for a given
application area; the variations will depend on what application
features are of interest and on how one choses to represent them in TF.
So there can be several different house-building or block-stacking
domains in the narrower sense of "domain". Each one typically
corresponds to a single TF source file, and these files / domains
have names such as "blocks-1" or "house-4".
The hypertext links in this document that are used to run O-Plan
look something like this:
- get-to-work
- task_get_to_work_via_expansion
- task_get_to_work_via_conditions
The links above will work; but you should read this before trying
them. The first line gives the domain, get-to-work. Select that
link to get the TF definition of the domain. The "task" lines
represent tasks or problems within the domain. Select a task
to cause O-Plan to run and produce a plan.
The get-to-work domain is a simple example designed to help explain
how O-plan works.
You may want to
read that explanation, at some point.
It also describes the outputs that O-Plan produces.
Now, here's a preliminary description of the example domains.
More complete descriptions, plus links for seeing the TF definitions
and for running O-Plan, will follow.
- Block stacking
-
Some TF files deal with various block
stacking problems such as the Sussman Anomaly.
- House Building
-
Several TF files define house building problems. The different files
deal with time constraints, alternative building methods and
contractors, etc.
- Missionaries and Cannibals
-
This is the standard missionaries and cannibals problem in which the
task is to move three missionaries and three cannibals from the right
bank of a river to the left bank using a single boat. The constraint is
that the cannibals should never outnumber the missionaries on
either bank (otherwise the cannibals will eat the missionaries!).
- Pacifica
-
Pacifica is an island state in the
Pacific and the tasks consist of moving a number of evacuees from
remote parts of the island to a central evacuation point and then
flying them out. This example can be used to demonstrate the AutoCAD
user interface to O-Plan (but not, unfortunately, on the Web).
- Satellite Control
-
A TF file for a satellite command and control problem. The satellite
has various experiments whose data must be captured and transmitted to
earth, taking into account time and resource constraints.
- Space Platform Construction
-
A TF file for a very simple space platform construction problem. This
example can be used to demonstrate the AutoCAD user interface to
O-Plan (though not via the Web).
Block Stacking
Block stacking puzzles are often used as a basic test domain for AI
planning systems. In this particular demonstration the planner will be
asked to solve the following type of problem:
_____
| |
| A |
_____ |_____|
| | | |
| C | | B |
|_____| _____ |_____|
| | | | | |
| A | | B | | C |
|_____| |_____| |_____|
Initial State Goal State
The planner is to construct a plan to change the initial state
into the goal state. This is a simple problem because the
planner has only a few simple plan operators which rely on the
following assumptions:
- The table on which the blocks sit can have as many blocks on top
of it as desired.
- The hand which moves the blocks can only move one block at a time.
- A block can only be moved if it has a clear top i.e. no other
block is on top of it.
- Any block which is the destination of a move must have a clear
top beforehand.
A full list of file names and task schema names are provided in the
following two tables. The file blocks-1 contains a single
puton schema with which the planner must construct a plan.
The file blocks-2 uses three schemas: a less capable
puton and two others: makeon and makeclear.
- blocks-1
-
- task_stack_abc
-
A
C ---> B (The Sussman Anomaly problem)
A B C
------ -----
- task_stack_abc_2
-
A
A ---> B
B C C
------ -----
- task_stack_cba
-
C
C ---> B
A B A
------ -----
- task_stack_bac
-
B
C ---> A
A B C
------ -----
- blocks-2
-
The problems are the same as in blocks-1, but the operators
used to solve them are different.
- task_stack_abc
-
A
C ---> B (The Sussman Anomaly problem)
A B C
------ -----
- task_stack_abc_2
-
A
A ---> B
B C C
------ -----
- task_stack_cba
-
C
C ---> B
A B A
------ -----
- task_stack_bac
-
B
C ---> A
A B C
------ -----
House Building
This application shows the development of a plan for the construction
of a typical family house. The plan is developed in a top-down manner
with high level actions such as install_services and
decorate being inserted first and then expanded.
This avoids the planner having to consider the detailed levels of the
plan before the more important high level actions have been sketched
out. The different house building tasks show how time and resources
can be modelled within the domain.
A full list of file names and task schema names are provided in the
following table.
- house-1
-
- task_build_house
- Builds a simple family house.
- house-2
-
- task_build_house
- Contains TF which shows how interactions occur between schemas
and how schemas which provide alternate ways of achieving a task
can be specified. The interaction can be seen in the plan trace
as a failure to expand the first install-services schema chosen
and as a result taking the second install-services schema instead.
- house-3
-
- task_build_large_house
- A larger house building example that in house-1 or house-2.
The plan constructed requires more condition satisfaction and
interaction removal than in the previous house building problems.
- house-4
- A house building example similar to house-1 except that it includes
durations for actions and time windows in which specified actions
must take place.
- task_build_house
- task_build_house_to_time_0
- Build the house within a set time period on difficult ground,
with the time limits so tight that no solutuion is possible.
- task_build_house_to_time_1
- Build the house within a set time period on ready ground,
1 alternative possible (with standard kitchen).
- task_build_house_to_time_2
- Build the house within a set time period on ready ground,
2 alternatives possible (one with standard kitchen, one with
luxury kitchen).
- three-pigs
- House-building constrained by strictly-consumable resources.
The resources available are money, sticks, straw and bricks.
(Guess who lives in this house.)
- task_build_house
- A simple family house with no restrictions on time and resources.
- task_build_secure_house
- Builds a family home for a cost between 0 and 2000 pounds which
is also proof against wolves.
- task_build_cheap_house
- Builds a home for a cost between 0 and 500 pounds.
- task_build_cheap_secure_house
- Builds a home for a cost between 0 and 500 pounds which is also
proof against wolves. (This turns out to be impossible.)
Missionaries and Cannibals
This is the standard missionaries and cannibals problem. The
definition shows some of the numerical reasoning capabilities of the
O-Plan system. The problem consists of moving 3 missionaries and 3
cannibals from the right bank of a river to the left bank using a single
canoe. The constraint on the problem is that the cannibals must never
outnumber the missionaries, for otherwise the missionaries will be
eaten.
The problem is defined in several different ways, as listed below.
All of them keep track of a "state" that lists the bank the boat is
on and the numbers of missionaries and cannibals on each side. All
record when a state has already been visited as a way to avoid
pointless journeys. However, they differ in how arithmetic is
performed or in the way they generate the sequence of moves. Some
of the techniques developed for this problem have later been used
in other domains.
The starting state has three missionaries and three cannibals
on the left back of the river along with the canoe.
- mission
-
The mathematics of calculating the number of missionaries and
cannibals is carried out using successor arithmetic based on matching
against patters that describe simple sums. Another set of patterns
describes the safe states.
- task_mc_problem
- Gets everyone to the right bank.
- mission-with-only-compute
-
The mathematics of calculating the number of missionaries and
cannibals is carried out using compute conditions that
call Common Lisp functions. Safety is checked in a similar way.
- task_mc_problem
- Gets everyone to the right bank.
- mission-forward-meta
-
This is the last written and most radical of the three.
- task_mc_problem
- Gets everyone to the right bank.
Pacifica
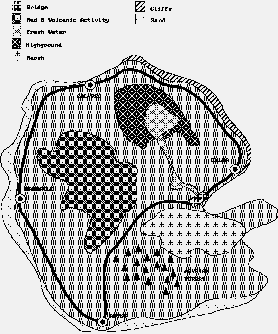
This example develops plans for evacuations from a hypothetical
island named Pacifica.
Pacifica is an island state located in the Pacific Ocean
within long distance flying time of Honolulu, Hawaii. It has a very
interesting coastline, but remains shrouded in mystery due to its
inaccessibility over the centuries. Only in the last century has it
been inhabited, though some areas of the island remain largely
unexplored and are unmapped.
The story
A number of people must be evacuated from the cities Abyss, Barnacle,
and Calypso. They will first be driven to the capital, Delta, then
flown to Honolulu. Initially, a C5, a B707, and some ground transports
(GTs) are located in Honolulu. From this initial situation, a plan is
developed that moves the required transportation resources from
Honolulu to Delta, uses the GTs to move the evacuees to Delta, and
finally flies everything to Honolulu.
A list of file names and task schema names are provided in the
following table.
- pacifica
-
- task_operation_blue_lagoon
- Two Ground Transports (GTs) are available.
Satellite Control
This application shows the development of a plan for the control of a
simple satellite we have called EUSAT (Edinburgh University
Satellite). This satellite is based on the actual University of
Surrey's successful UoSAT series of satellites. Earlier research into
the application of task planning and scheduling at Edinburgh has
included work on defining a task formalism description for O-Plan1 for
a spacecraft similar to UoSAT-II but omitting confidential information
(which we called BOGUSAT). This was further extended in the T-SCHED
scheduling system, which took a scheduling perspective as opposed to
the task planning view of O-Plan1, and generated actual on-board
computer Diary commands. The O-Plan project EUSAT model uses the
same spacecraft model as BOGUSAT.
The experiments of the spacecraft include:
- Navigational Magnetometer (NAVMAG)
- Sun Sensor
- Horizon Sensor
- Space Dust Analyser
- Digital Voice Recording (DigiTalker)
- Charge Coupled Device (CCD)
- Particle Wave Experiment
The experiments are connected via a series of switches to a tape
recorder (DSR) and then to either a 70cm or 2m
antenna for transmission to the ground. Alternatively some experiments
can be connected directly to an antenna through line6
instead of passing through the DSR. One of the experiments,
called the DigiTalker, allows for a message to be loaded into a tape
recorder (the DCE) from the ground and subsequently
re-transmitted at a later time back to the ground. As well as the
series of experiments, the satellite must also send telemetry data to
the ground.
The movement of data from an experiment to an antenna is modelled as a
set of switch settings. Each switch has a valid set of inputs and
outputs, as follows:
Switch No Inputs Outputs
--------- ------ -------
1 line0 line1 line2 line3 line4 line5
2 line5 line6 line7
3 line7 line8 line9 line10
4 line6 line12 line13 line15 line 16
5 line16 antenna70cm antenna2m
6 antenna70cm antenna2m ground buffer
A task given to O-Plan describes the requirements for work in a
typical day in the life of the spacecraft.
- monitor_spacecraft_health: Send current telemetry data to ground.
- capture CCD: Collect data from the CCD and send it
to the ground via the DSR.
- capture p_w: Collect data from the particle wave
experiment and send it to the 2m antenna either
directly or via the DSR.
- capture space_dust: Collect data from the space dust
analyser and send it to the 2m antenna either directly
or via the DSR.
- DCE_communicate: Receive and re-send a message from and
back to ground.
The task specifies the objectives of the mission. This is a series of
experiments whose data must be collected and transmitted to a ground
buffer via one of two antennas. O-Plan is able to generate a plan for
such a mission and give output in a form that could be accepted by the
normal diary based dispatch execution system on board a simple
spacecraft.
The following table describes the files and task schemas which are
available in this domain.
- eusat
-
- task_mission_objectives_1
- Capture the data from a series of experiments and transmit it
to a ground buffer. The order of the data capture is specified
by the user and is sequential.
- task_mission_objectives_2
- Similar to the task above except that the order of data capture
is unspecified.
The O-Plan planning agent has been demonstrated generating a plan for
such a task and passing it to an O-Plan architecture based execution
system for simple dispatch and monitoring to take place.
Other related work at Edinburgh has led to the two planning systems
for the European Space Agency. The first was the Plan-ERS
system which could generate mission plans for the European Space
Agency's ERS-1 spacecraft. This prototype was built in the KEE
knowledge representation system and uses a simple plan representation.
A second system, OPTIMUM-AIV, is able to generate and support the
execution of plans for spacecraft assembly, integration and
verification. This second planner uses a Goal Structure based plan
representation working alongside links to a traditional project
management support system (ARTEMIS).
Space Platform Construction
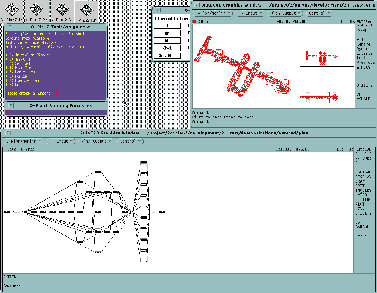
This application shows the development of a plan for the construction
of one of a number of different Space Platforms. Platforms are
constructed from a series of joints, trusses, pressurised modules,
solar panels, radiators and antennas.
This domain is normally used to demonstrate the AutoCAD user interface
that has been constructed for O-Plan. AutoCAD can draw a PostScript
picture (like
this one) of a platform at any point in its construction, based
on information from a complete or developing plan. A screen dump of
the AutoCAD interface is shown above. (Select the picture to see a
larger version.)
The following list describes the files and task schemas which
are available in this domain.
- space-platform
-
- task_space_platform
- Builds a medium sized space platform with 1 antenna, 4 solar panels,
2 radiators, 2 modules, 3 trusses and 3 joints.
- task_small_space_platform
- Builds a small sized space platform with 1 antenna, 2 solar panels,
1 radiator, 1 module and 1 joint.
- task_large_space_platform
- Builds a large sized space platform with 2 antenna, 6 solar panels,
2 radiators, 5 modules, 4 trusses, 3 tubes and 8 joints.
Creating and Running your own Applications
Unfortunately, you can't yet run your own applications over the Web,
but we hope to change that soon.
The TF language allows users to develop their own applications.
Some of the demonstration applications could be used as starting
points. This section provides only a brief introduction and
overview of what goes in a TF description file.
Task Schemas
The task schemas introduce the tasks the planner is asked to carry
out. The first line of a task definition begins with task
to indicate to the planner that it is a task schema. Other schema
definitions begin with schema. Here's a sample task:
task build_stack_ABC;
nodes 1 start,
2 finish;
orderings 1 ---> 2;
conditions achieve {on a b} = true at 2,
achieve {on b c} = true at 2;
end_task;
This task schema provides an initial plan: start and finish nodes,
which are always numbered 1 and 2 respectively. The orderings
clause says that the start (1) must be before the finish (2).
The conditions clause indicates to the planner any conditions
it must achieve. In the example above there are two conditions to
achieve by the finish of the plan (i.e., "at 2") which together represent
a three-block tower: a b c.
A task schema can also be used to provide a high level action
which the planning system must expand into progressively lower level
actions until an executable plan is available. In the example below the
action to be expanded is to build a house:
task build_house;
nodes 1 start,
2 finish,
3 action {build house};
orderings 1 ---> 3, 3 ---> 2;
end_task;
Global Data and Object Types
These data items specify the objects in the domain and the classes to
which they belong. They also declare specific statements which
cannot be refuted by the effects of plan actions actions. These are
referred to as "always statements" or "always facts".
In the block stacking domain the following global data
could be specified:
always {cleartop table} = true; ;;; the table is always a clear object
types objects = (a b c table), ;;; all objects in the domain
movable_objects = (a b c); ;;; stop the planner trying to
;;; move the table
Application Schemas
The application schemas provide the "actions" of the plan together
with information concerning variables, resources, time windows and
domain information to help in search control. The schema below defines
an action which puts one object on top of another, i.e.
{puton ?x ?y}. Information concerning the variables
?x and ?y is given in two different places:
- vars
-
This statement introduces the variables of the schema together with
their types (if known) and other relationships. The type is an
enumerated set which allows the planner to determine all possible
values the variable could take.
- var_relations
-
This statement introduces the equality and inequality relationships
between variables in the schema. In the example below the /=
(not-equal) relationship stops the planner binding the object being
moved and the destination of the move to the same value.
schema puton;
vars ?x = ?{type movable_objects},
?y = ?{type objects},
?z = ?{type objects};
var_relations ?x /= ?y, ?x /= ?z, ?y /= ?z;
expands {puton ?x ?y};
only_use_for_effects
{on ?x ?y} = true,
{cleartop ?y} = false,
{on ?x ?z} = false,
{cleartop ?z} = true;
conditions only_use_if {cleartop ?x},
only_use_if {cleartop ?y},
only_use_for_query {on ?x ?z};
end_schema;
The conditions statement specifies condition types
that tell the planner how a particular condition should be satisfied.
This also provides the planner with information as to the strength
of commitment to maintaining the condition in a particular way.
The names only_use_if, only_use_for_query, and
(in one of the tasks above) achieve are all condition types.
A complete list of condition types is described in the TF
Manual.
The only_use_for_effects and effects statements
inform the planner of the effects the schema asserts. The
only_use_for_effects statement indicates the effects which
the schema can be used to achieve, i.e. its primary effects. The
effects statement indicates the side effects of the action.
The schema should not be chosen specifically to achieve them.
The sections above give a brief overview. Facilities such as
resources and time windows have not been described but are fully
documented in the TF Manual.
Jeff Dalton
Brian Drabble

