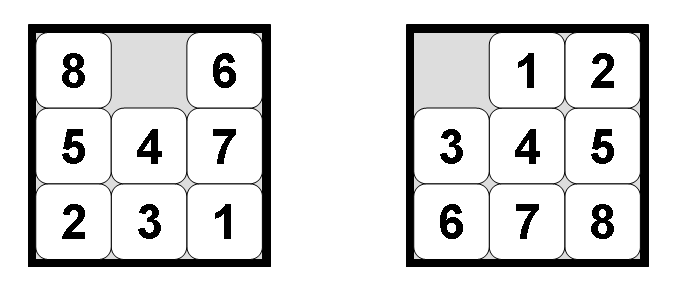
Figure 1: Configurations of the 8-Puzzle: worst-case initial state (left) for goal state (right)
The 8-puzzle is a smaller version of the slightly better known 15-puzzle. The puzzle consists of an area divided into a grid, 3 by 3 for the 8-puzzle, 4 by 4 for the 15-puzzle. On each grid square is a tile, expect for one square which remains empty. Thus, there are eight tiles in the 8-puzzle and 15 tiles in the 15-puzzle. A tile that is next to the empty grid square can be moved into the empty space, leaving its previous position empty in turn. Tiles are numbered, 1 thru 8 for the 8-puzzle, so that each tile can be uniquely identified.
The aim of the puzzle is to achieve a given configuration of tiles from a given (different) configuration by sliding the individual tiles around the grid as described above.
This problem can be solved by searching for a solution, which is a sequence of actions (tile moves) that leads from the initial state to the goal state. Two possible states of the 8-puzzle are shown in figure 1. The state on the right is a typical goal state. The state on the left is a configuration that represents a worst case: transforming this state into the goal state requires at least 31 actions, which is the diameter of the search space. For search algorithms the problem is often to find the shortest solution, that is, one which consists of the least number of tile moves.

Figure 1: Configurations of the 8-Puzzle: worst-case initial state (left) for goal state (right)
HeuristicEightPuzzleApp is a Java application that explores the above search space using a number of (informed) search strategies. Download the application and double-click it. Alternatively, run the command "java -jar HeuristicEEightPuzzleApp.jar" from the command line. Either should bring up a window that looks essentially like the one shown in figure 2.

Figure 2: The window of the application
To search for a solution, first select a search strategy. Next, there are some configuration options for the search process. If the search space is to be searched as a graph, multiple paths leading to the same node will usually only be explored once. In a tree, search states that can be reached by multiple paths will also be explored multiple times. Heuristic search also requires a heuristic, which must be specified. Currently, the only implemented heuristic is the Manhattan block distance heuristic, which is admissible. Also, it is possible to assign a weight to the heuristic, which is a factor applied to the h-value during the search. Not all types of search engine support this feature. The number of states to be generated can be limited to the given value, resulting in the search being abandoned at that point.
To start the serach press the Step or Search button. This will bring up a dialog box that confirms the input state. The default value is the left puzzle in figure 1 represented as the string:
8 0 6 5 4 7 2 3 1
This string is simply a line by line enumeration of the tile numbers, where 0 (zero) represents the empty space. Type in a different state if required or accept the current state.
Finally, a trace of the search can be written to the window and/or a text file. Note that this may cause the JVM to run out of memory if the trace is written to the window! The operation performed by a search engine consists of selecting a current search node and generating its successors, and the trace reflects this process. Note that the exact trace differs depending on the search strategy chosen. For example, using A*, the line:
current state: 4: <State: 8 0 6 5 4 7 2 3 1> (f=21)
indicates that the selected node contains the given state. The number (4 in the example) is the unique identifier for the search node. Note that there may be multiple nodes that contain the same state, especially when tree search is performed. Then there is a description of the selected state which is similar to the input, namely a line by line enumeration of the tiles. Finally, there is the f-value of this node. The lines following this one in the trace describe the successor states that have been generated, for example:
successor state (f=21): <Move: West> 5: <State: 0 8 6 5 4 7 2 3 1> successor state (f=23): <Move: South> 6: <State: 8 4 6 5 0 7 2 3 1> successor state (f=21): <Move: East> 7: <State: 8 6 0 5 4 7 2 3 1>
So, expanding the given search node (4) resulted in two new search nodes (5, 6 and 7).
Even with tracing off the window will display some information about the search (which is not part of the trace). It will show how many states have been explored (the goal test has been performed and successors have been generated) and how many states have been generated (explored states plus fringe nodes). If a solution is found this will also be printed. Finally, the elapsed time taken to perform the search is printed. Note that writing the trace usually takes more time than searching itself.
S. Russell and P. Norvig. Artificial Intelligence: A Modern Approach, chapter 4. Prentice Hall, 2nd edition, 2003.